Traccia

Svolgimento

Qui dovremo analizzare 3 casi, studiano prima sul grafico i comportamenti dei singoli valori assoluti:

• 
• 

	—-	—-	+++
	—-	+++	+++

 

Quindi dobbiamo studiare 3 sistemi, e dove segnalato, cambiare i segni ai valori assoluti:

• Primo sistema:

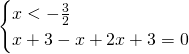
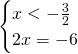
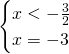
Questa soluzione è accettabile.

• Secondo sistema:

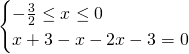
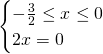
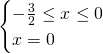
Questa soluzione è accettabile.

• Terzo sistema:

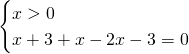
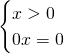
L’equazione è indeterminata, quindi vuol dire che questo sistema ammette come soluzione proprio .

 

Unendo le 3 soluzioni, otteniamo la soluzione totale che è:

 

 

Altri esercizi simili:

• Esercizio 1 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 2 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 3 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 4 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 5 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 6 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 7 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 8 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 9 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 10 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 11 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 12 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 13 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 14 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 15 Equazioni in cui figurano valori assoluti di espressioni contenenti l’incognita

(Questa pagina è stata visualizzata da 199 persone)