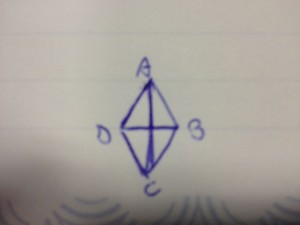
Svolgimento problema di geometria piana risolubile con equazioni di primo grado
- La somma delle diagonali di un rombo è 60 cm e i
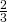 della maggiore aggiunti alla metà della minore danno 36 cm. Determinare l’area del rombo.
della maggiore aggiunti alla metà della minore danno 36 cm. Determinare l’area del rombo.
Dai dati e dal disegno otteniamo, ponendo ![]() :
:
![]()
![]()
Dalla prima otteniamo:
![]() (ometto per comodità le unità di misura..)
(ometto per comodità le unità di misura..)
Sostituendo quindi nella seconda otteniamo:
![]()
![]()
![]()
![]()
![]()
Da cui:
![]() .
.
E dunque:
![]()
Altri esercizi simili:
- Problema 1
- Problema 2
- Problema 3
- Problema 4
- Problema 5
- Problema 6
- Problema 7
- Problema 8
- Problema 9
- Problema 10
- Problema 11
- Problema 12
- Problema 13
(Questa pagina è stata visualizzata da 615 persone)