Problema 12

-4

Svolgimento problema di geometria piana risolubile con equazioni di primo grado

 

  1. In un trapezio isoscele il rapporto delle basi è 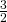\frac 3 2 e il lato obliquo è i 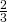\frac 2 3 della base minore. Determinare il perimetro del trapezio sapendo che la somma tra la base maggiore e metà del lato obliquo è 66 cm.

 

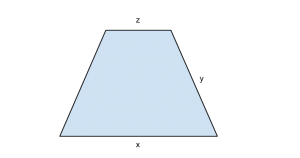
trapezioisoscele

 

Dai dati e dal disegno otteniamo:

\frac z x = \frac 3 2

y=\frac 2 3 x

z+\frac 1 2 y=66 \mbox{ cm}

Dalla prima otteniamo che:

z=\frac 3 2 x

Sostituendo la prima e la seconda nella terza equazione otteniamo:

\frac 3 2 x + \frac 1 2 \frac 2 3 x = 66 (ometto le unità di misura per comodità)

\frac 3 2 x + \frac 1 3 x = 66

\frac {9+2} 6 x=66

\frac {11}{6} x = 66

x=\frac 6 {11} 66 \mbox{ cm}=36 \mbox{ cm}

Da cui:

y=\frac 2 3 x =\frac 2 3 36 \mbox{ cm} = 24 \mbox{ cm}

z=\frac 3 2 x= \frac 3 2 36 \mbox{ cm} = 54 \mbox{ cm}.

Quindi il perimetro sarà:

2p=(54+36+24+24) \mbox{ cm}=138 \mbox{ cm}

 

 

 

Altri esercizi simili:

 

 

(Questa pagina è stata visualizzata da 676 persone)

2 pensieri riguardo “Problema 12”

  1. Mi permetto di segnalare un errore di calcolo riferito a z (base maggiore), che è 3/2 di x (36); il dato risultante è 54 (36:2×3) e non 48. Anche la misura del perimetro, di conseguenza, cambia ed è 138, non 132. Grazie

Lascia un commento