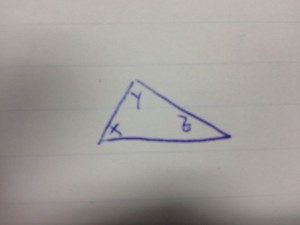
Svolgimento problema di geometria piana risolubile con equazioni di primo grado
Determinare gli angoli di un triangolo sapendo che il primo è ![]() del secondo e che il terzo angolo supera di 30° la somma degli altri due.
del secondo e che il terzo angolo supera di 30° la somma degli altri due.
Sappiamo che la somma degli angoli di un triangolo è ![]() . Quindi, osservando il disegno, otteniamo:
. Quindi, osservando il disegno, otteniamo:
![]()
![]()
![]()
Sostituendo queste ultime due nella prima otteniamo:
![]()
![]()
![]()
![]()
Per cui:
![]()
![]() .
.
Altri esercizi simili:
- Problema 1
- Problema 2
- Problema 3
- Problema 4
- Problema 5
- Problema 6
- Problema 7
- Problema 8
- Problema 9
- Problema 10
- Problema 11
- Problema 12
- Problema 13
(Questa pagina è stata visualizzata da 532 persone)