Problemi sui teoremi di Euclide

-11

Tracce

  1. In un triangolo rettangolo il cateto minore è 90 cm, la sua proiezione sull’ipotenusa è 9/25 della stessa ipotenusa. Determinare il perimetro e l’area del triangolo. Indicare con x la misura dell’ipotenusa. 
  2. In un triangolo rettangolo un cateto è lungo 45 cm e la sua proiezione sull’ipotenusa è i 9/16 della proiezione dell’altro cateto sull’ipotenusa. Trovare perimetro e area del triangolo. (Indicare con x la misura della proiezione…)
  3. Nel triangolo isoscele ABC la base BC è lunga 120 cm e la proiezione BD della metà base BH sul lato AB è i 9/25 dello stesso lato AB. Calcolare il perimetro e l’area del triangolo. Porre AB=x.
  4. In un triangolo rettangolo un cateto è 4/5 dell’ipotenusa e il perimetro è di 96 cm. Determinare l’ipotenusa e le proiezioni dei cateti sull’ipotenusa.
  5. In un triangolo rettangolo la proiezione di un cateto sull’ipotenusa è 9/25 dell’ipotenusa stessa e l’altezza relativa all’ipotenusa è lunga 48m. Determinare l’ipotenusa.
  6. I cateti AB e AC di un triangolo rettangolo ABC misurano, in centimetri, rispettivamente 10 e 24. Determinare la misura delle loro proiezioni sull’ipotenusa.
  7. Il triangolo ABC è rettangolo in C e l’altezza CH relativa all’ipotenusa è lunga 24 cm e divide l’ipotenusa stessa in parti AH e HB tali che AH=9/16 HB. Determinare perimetro e area del triangolo.
  8. In un triangolo rettangolo il cateto maggiore è 120 cm, la sua proiezione sull’ipotenusa è i 16/25 della stessa ipotenusa. Determinare perimetro e area del triangolo.
  9. In un triangolo rettangolo un cateto è lungo 60 cm e la sua proiezione sull’ipotenusa è i 4/3 dell’altezza relativa all’ipotenusa. Trovare il perimetro e l’area del triangolo.
  10. Del rettangolo ABCD si conosce la diagonale (AC=17 cm) e un lato (AB=8 cm). Determinare la proiezione CH del lato BC sulla diagonale AC.
  11. Nel triangolo rettangolo ABC, l’altezza AH condotta dal vertice A dell’angolo retto divide l’ipotenusa BC in due segmenti di 18 cm e 50 cm. Determinare AH e il perimetro del triangolo.
  12. In un triangolo rettangolo l’ipotenusa è di 20 cm e l’altezza a essa relativa di 9,6 cm. Determinare le lunghezze dei cateti.
  13. In un triangolo rettangolo l’altezza relativa all’ipotenusa è di 6 cm e le proiezioni dei cateti sull’ipotenusa differiscono di 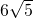6\sqrt5 cm. Determinare l’area del triangolo.
  14. I cateti AB e AC di un triangolo rettangolo soddifsano la relazione 2AB+AC=2a. Sia E il punto in cui la retta AB incontra la perpendicolare in C all’ipotenusa. Sapendo che BE=a, determinare i cateti AB e AC del triangolo considerato.
  15. In un rettangolo la base supera di 4 cm i 2/3 dell’altezza e l’area è 48 cm^2. Determinare le lunghezze dei lati, della diagonale e il rapporto tra i segmenti in cui viene divisa la diagonale dalla proiezione ortogonale di uno dei vertici sulla diagonale stessa.
  16. Inscrivere in un semicerchio, il cui raggio è di 9 cm, un triangolo rettangolo, avente per ipotenusa il diametro, in modo che il rapporto tra un cateto e la sua proiezione sull’ipotenusa sia \frac 23 \sqrt 3.
  17. In un trapezio rettangolo ABCD la diagonale minore AC è perpendicolare al lato BC. Sapendo che la base minore CD è di 32 cm e l’altezza AD di 24 cm, calcolare il perimetro del trapezio.
  18. In un trapezio rettangolo la diagonale minore è perpendicolare al lato obliquo. Sapendo che le due basi sono di 50 cm e 18 cm, trovare il perimetro e l’area del trapezio.
  19. Nel triangolo rettangolo ABC la proiezione HB del cateto AB sull’ipotenusa BC misura 4a. Sapendo che 2HC-.AB=HB, si determini la misura del perimetro del triangolo ABC. ( se si pone AB=x, si trova l’equazione x^2-2ax-24a^2=0…)
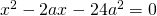  20. E’ data una semicirconferenza di diametro AB=25 cm e sul diametro AB due punti H e K tali che AH=9 cm e BK=8 cm. Da H e K si conducono le perpendicolari al diametro che incontrano rispettivamente in C e in D la semicirconferenza. Determinare CH,AC,BD,BC,AD.
  21. Determinare la misura del perimetro del trapezio isoscele ABCD inscritto in una semicirconferenza di diametro AB, sapendo che la misura della diagonale AC è 24a e che, detta HB la proiezione del lato BC sulla base maggiore AB, è HB=50/13 a. (Posto AB=x, con x>24a, l’equazione risolvente si trova subito applicando il 1° teorema di Euclide al triangolo ABC; si otterrà l’equazione 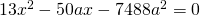13x^2-50ax-7488a^2=0 di cui è accettabile solo una soluzione…)
  22. In un trapezio isoscele ciascuna diagonale è perpendicolare al lato obliquo, La somma delle basi misura, in centimetri, 128 e una è i 7/25 dell’altra. Determinare la misura del perimetro e dell’area del trapezio.
  23. Dopo aver calcolato la misura della base di un triangolo isoscele, di altezza lunga 96 cm, circoscritto a un cerchio il cui raggio è di 21 cm, determinare la misura del raggio del cerchio circoscritto al triangolo.
  24. Un triangolo isoscele è inscritto in una circonferenza di raggio 75 cm e la sua altezza è i 16/25 del diametro. Determinare i lati del triangolo.
  25. Data una semicirconferenza di diametro AB=2r, determinare un punto C sopra di essa in modo che, indicata con H la sua proiezione su AB, risulti: 2AH^2 + 6CH^2=9r^2.

(Questa pagina è stata visualizzata da 1727 persone)

2 pensieri riguardo “Problemi sui teoremi di Euclide”

  1. Pingback: Teoremi di Euclide | Matebook

Lascia un commento