Tracce:
- Determinare per quali valori del parametro reale k le seguenti equazioni hanno soluzioni reali:

- Determinare per quali valori del parametro reale k le seguenti equazioni hanno soluzioni reali:
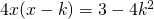
- Determinare per quali valori del parametro reale k le seguenti equazioni hanno soluzioni reali:
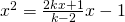
- Determinare per quali valori del parametro reale k le seguenti equazioni hanno soluzioni reali:
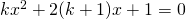
- Stabilire per quali valori di b l’equazione
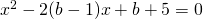 non ha soluzioni in
non ha soluzioni in 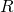 .
. - Determinare k in modo che l’equazione
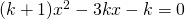 abbia due soluzioni distinte.
abbia due soluzioni distinte. - Dopo aver verificato che l’equazione
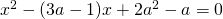 ha sempre soluzione per qualsiasi valore di a, determinare a in modo che le due radici siano entrambe positive.
ha sempre soluzione per qualsiasi valore di a, determinare a in modo che le due radici siano entrambe positive. - Determinare i valori del parametro m per cui l’equazione
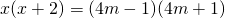 ha due soluzioni distinte, entrambe negative.
ha due soluzioni distinte, entrambe negative. - Determinare i valori del parametro k per cui l’equazione
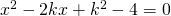 ha due soluzioni concordi, dopo aver verificato che l’equazione ha sempre due soluzioni.
ha due soluzioni concordi, dopo aver verificato che l’equazione ha sempre due soluzioni. - Determinare i valori del parametro k per cui l’equazione
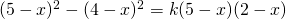 ha due soluzioni discordi, dopo aver verificato che l’equazione ammette sempre due soluzioni.
ha due soluzioni discordi, dopo aver verificato che l’equazione ammette sempre due soluzioni. - Data l’equazione:
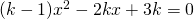 , determinare k in modo che essa ammetta soluzioni concordi.
, determinare k in modo che essa ammetta soluzioni concordi. - Dire per quali valori di k le soluzioni dell’equazione
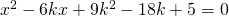 sono concordi.
sono concordi. - Data l’equazione
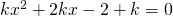 , stabilire per quali valori di k le radici sono discordi.
, stabilire per quali valori di k le radici sono discordi. - Data l’equazione
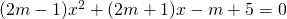 , determinare i valori di m per cui si hanno soluzioni tali che il loro prodotto sia maggiore di -2/5.
, determinare i valori di m per cui si hanno soluzioni tali che il loro prodotto sia maggiore di -2/5. - Stabilire per quali valori di a l’equazione
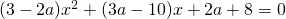 ammette soluzioni che verificano la relazione:
ammette soluzioni che verificano la relazione: 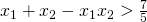 .
. - Verificare che, per i valori di k per i quali l’equazione
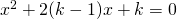 ha soluzioni, anche l’equazione
ha soluzioni, anche l’equazione 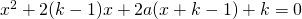 ammette radici reali,
ammette radici reali, 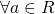 .
. - Determinare per quali valori di k la somma delle soluzioni reali dell’equazione
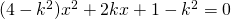 è maggiore di 3.
è maggiore di 3.
Altri hanno visualizzato anche
- Equazioni omogenee di secondo grado in seno e coseno
- Esercizi equazioni di secondo grado
- Esercizi equazioni di secondo grado incomplete
- Esercizi equazioni di secondo grado letterali frazionarie
- Esercizi equazioni di secondo grado letterali intere
- Esercizi equazioni di secondo grado: Problemi di geometria piana
- Esercizi equazioni di secondo grado: Problemi di secondo grado
- Esercizi equazioni frazionarie numeriche
- Esercizi equazioni intere numeriche
- Esercizi Equazioni parametriche
- Scomposizione del trinomio di secondo grado
- Valori assoluti: equazioni in cui compaiono valori assoluti
(Questa pagina è stata visualizzata da 1527 persone)