Traccia

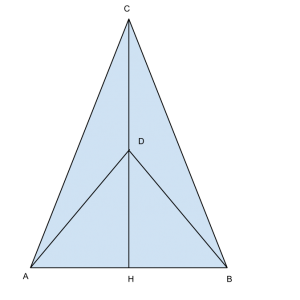
In un triangolo isoscele la base supera ciascuno dei lati congruenti di 3 dm e il perimetro è di 48 dm. L’altezza relativa alla base e i due segmenti che congiungono il punto medio di tale altezza con gli estremi della base dividono il triangolo in quattro parti. Determinare l’area di ciascuna di esse.

Svolgimento

 

 

Dai dati avremo:

Imponendo che , otteniamo subito:

da cui:

Troviamo CH con il teorema di Pitagora:

Quindi:

.

Troviamo l’area del triangolo rettangolo :

Adesso calcoliamo l’area del triangolino ADH, equivalente al triangolino BHD.

Ma quindi anche gli altri due triangoli avranno proprio la stessa area, quindi:

 

 

 

 

 

Altri esercizi simili

• Esercizio 1 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 2 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 3 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 4 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 5 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 6 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 7 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 8 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 9 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 10 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 11 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 12 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 13 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 14 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 15 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 16 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 17 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 18 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 19 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 20 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 21 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 22 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 23 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 24 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 25 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
• Esercizio 26 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora

(Questa pagina è stata visualizzata da 178 persone)