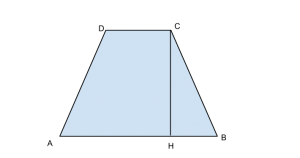
Traccia
La differenza delle basi di un trapezio isoscele è 60 cm e la somma è 68 cm. Determinare l’area del trapezio sapendo che il lato obliquo è di 34 cm.
Svolgimento
Dai dati avremo che:
![]()
![]()
![]()
Ipotizzando un sistema, possiamo sommare le prime due equazioni così da ottenere:
![]()
![]()
![]() ,
,
e quindi:
![]() .
.
Per calcolare l’area ci serve ricavare l’altezza sapendo che:
![]()
e sfruttando il teorema di pitagora, otteniamo:
![]() ;
;
l’area sarà:
![]()
Altri esercizi simili
- Esercizio 1 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 2 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 3 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 4 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 5 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 6 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 7 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 8 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 9 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 10 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 11 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 12 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 13 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 14 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 15 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 16 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 17 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 18 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 19 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 20 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 21 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 22 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 23 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 24 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 25 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 26 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
(Questa pagina è stata visualizzata da 82 persone)