Traccia
Un trapezio isoscele è diviso dalla parallela al lato obliquo, condota per uno degli estremi della base minore, in un triangolo e in quadrilatero il cui rapporto è 2/5. Sapendo che l’altezza è di 3 cm. e che l’area del trapezio è 42 cm![]() , determinare il perimetro del trapezio dato. Condurre dal punto medio di uno dei lati obliqui la parallela alle basi e determinare perimetro e area del trapezio formato da tale parallela e dalla base maggiore del trapezio dato.
, determinare il perimetro del trapezio dato. Condurre dal punto medio di uno dei lati obliqui la parallela alle basi e determinare perimetro e area del trapezio formato da tale parallela e dalla base maggiore del trapezio dato.
Svolgimento
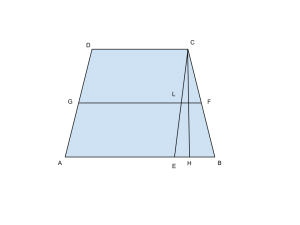
Dal grafico notiamo subito che il triangolo CBE è isoscele per costruzione, e il quadrilatero AECD è un parallelogrammo. Denotiamo con ![]() l’area del parallelogrammo così da avere:
l’area del parallelogrammo così da avere:
![]()
Ovviamente l’area del trapezio è dato dalla somma delle due aree e quindi:
![]()
![]()
![]()
Così avremo che:
![]()
![]()
Conoscendo l’altezza possiamo ricavare le basi del triangolo e del parallelograma:
![]()
![]()
![]()
![]()
Avremo quindi che:
![]()
Per trovare la base minore imponiamo che :
![]()
![]()
e quindi:
![]()
Per il lato obliquo basterà usare Pitagora:
![]()
Possiamo ora calcolare il permietro del trapezio:
![]()
Del trapezio seguente conosciamo:
![]()
![]()
Per calcolare la base minore, basti notare che i triangoli ECB e CFL sono simili con coefficiente di similitudine 2, e quindi avremo proprio che:
![]()
e ora la base minore sarà:
![]()
Il nuovo perimetro sarà:
![]()
e l’area:
![]()
Altri esercizi simili
- Esercizio 1 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 2 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 3 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 4 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 5 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 6 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 7 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 8 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 9 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 10 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 11 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 12 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 13 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 14 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 15 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 16 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 17 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 18 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 19 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 20 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 21 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 22 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 23 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 24 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 25 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 26 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
(Questa pagina è stata visualizzata da 308 persone)
grazie mille per l’ottimo vavoro che svolgete con questo sito! potrei sapere da che libro è stato tratto questo esercizio?