Traccia
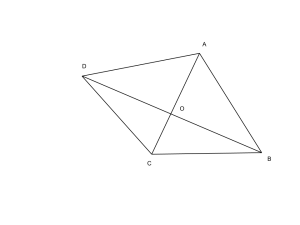
Il quadrilatero ABCD ha le diagonali, che si incontrano nel punto O, perpendicolari tra loro; si conosce che il perimetro del quadrilatero è di 56 cm, che ![]() ,
, ![]() e
e ![]() . Determinare l’area del quadrilatero ABCD.
. Determinare l’area del quadrilatero ABCD.
Svolgimento
Dai dati avremo che:
![]()
![]()
![]()
![]() e
e
![]() .
.
Innanzitutto poniamo ![]() , così da ottenere:
, così da ottenere:
![]()
![]()
Per costruzione, avremo quattro triangoli rettangoli uguali a due a due, ovvero avremo che:
![]() e
e
![]() .
.
Ricaviamo AB, che tra l’altro è uguale ad AD, in funzione di x con il teorema di Pitagora:
![]()
Ricaviamo allo stesso modo BC, segmento uguale a CD:
![]()
Ora che abbiamo tutti e 4 i lati in funzione di x, possiamo sfruttare l’uguaglianza al perimetro:
![]()
![]()
![]()
Da cui avremo:
![]()
![]()
![]()
Le diagonali saranno quindi:
![]()
![]()
L’area sarà quindi:
![]()
Altri esercizi simili
- Esercizio 1 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 2 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 3 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 4 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 5 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 6 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 7 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 8 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 9 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 10 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 11 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 12 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 13 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 14 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 15 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 16 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 17 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 18 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 19 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 20 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 21 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 22 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 23 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 24 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 25 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 26 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
(Questa pagina è stata visualizzata da 160 persone)