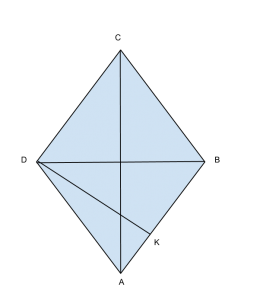
Traccia
L’area di un rombo è 960 dm![]() e il rapporto tra le sue diagonali è 15/8. Determinare il perimetro e l’altezza del rombo.
e il rapporto tra le sue diagonali è 15/8. Determinare il perimetro e l’altezza del rombo.
Svolgimento
Dai dati abbiamo che:
![]()
![]()
Poniamo ![]() , e otteniamo:
, e otteniamo:
![]()
e quindi:
![]()
![]()
![]()
![]()
Da cui abbiamo:
![]()
![]()
Col teorema di Pitagora ricaviamo un qualsiasi lato del rombo e avremo:
![]()
Possiamo ora calcolare il perimetro del rombo:
![]()
Per trovare l’altezza sfruttiamo la formula inversa sull’area di metà rombo, e quindi:
![]()
e quindi l’altezza sarà:
![]() .
.
Altri esercizi simili
- Esercizio 1 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 2 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 3 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 4 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 5 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 6 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 7 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 8 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 9 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 10 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 11 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 12 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 13 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 14 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 15 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 16 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 17 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 18 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 19 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 20 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 21 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 22 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 23 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 24 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 25 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
- Esercizio 26 Problemi risolubili con equazioni di primo grado e con l’applicazione del teorema di Pitagora
(Questa pagina è stata visualizzata da 164 persone)