Problemi teorema di Pitagora

-12

Tracce

  1. Di un triangolo ABC rettangolo in A, determinare perimetro e area dove:

        \[AB+AC=84 \mbox { cm } \quad \mbox { e } \quad AC=\frac 43 AB\]

    .

  2. Di un triangolo ABC rettangolo in A, determinare perimetro e area dove:

        \[BC+AC=256 \mbox { cm } \quad \mbox { e } \quad BC=\frac {17}{15} AC\]

    .

  3. Di un triangolo ABC rettangolo in A, determinare perimetro e area dove:

        \[AB=\frac 45 \mbox { e } \quad BC=36 \mbox { cm }\]

    .

  4. La base di un rettangolo è i 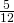\frac {5}{12} della sua altezza e la loro differenza è 42 cm. Determinare perimetro e area del rombo che si ottiene congiungendo successivamente i punti medi dei lati del rettangolo.
  5. Un trapezio isoscele è diviso dalla parallela al lato obliquo, condota per uno degli estremi della base minore, in un triangolo e in quadrilatero il cui rapporto è 2/5. Sapendo che l’altezza è di 3 cm. e che l’area del trapezio è 42 cm^2, determinare il perimetro del trapezio dato. Condurre dal punto medio di uno dei lati obliqui la parallela alle basi e determinare perimetro e area del trapezio formato da tale parallela e dalla base maggiore del trapezio dato.
  6. Il perimetro del triangolo ABC, isoscele sulla base BC, è di 64 cm e la base BC supera di 13 cm ciascuno dei lati congruenti AB e AC. Determinare l’area del triangolo. Sia D il punto medio di AC e D’ il simmetrico di D rispetto a BC; detto A’ il punto simmetrico di A rispetto a BC, determinare perimetro e area del trapezio ADD’A’.
  7. Un triangolo isoscele ha il perimetro di 384 m e la base è i 14/25 di ciascun lato. Calcolare l’area del triangolo.
  8. Un triangolo isoscele ha l’area di 108 cm^2 e l’altezza è i 2/3 della base. Determinare il perimetro del triangolo e le altezze relative ai lati congruenti.
  9. Il perimetro di un triangolo isoscele è lungo 36 dm; il rapporto tra un lato e metà base è 5/4. Determinare l’area del triangolo e la distanza del piede dell’altezza relativa alla base da ognuno dei lati obliqui.
  10. In un triangolo isoscele la base supera ciascuno dei lati congruenti di 3 dm e il perimetro è di 48 dm. L’altezza relativa alla base e i due segmenti che congiungono il punto medio di tale altezza con gli estremi della base dividono il triangolo in quattro parti. Determinare l’area di ciascuna di esse.
  11. Un rettangolo ha il perimetro di 320 cm e un lato è i 3/2 dell’altro. Calcolare l’area del rettangolo e le distanze del punto di intersezione delle diagonali dai vertici.
  12. In un rettangolo, avente il perimetro di 70 cm, il lato maggiore supera di 10 cm i 2/3 del lato minore. Determinare l’area e la diagonale del rettangolo.
  13. Il rapporto tra i lati di un rettangolo è 8/15 e il perimetro è 138 cm. Determinare l’area del rettangolo e la sua diagonale. Dimostrare poi che, congiungendo i punti medi dei suoi lati, si ottiene un rombo il cui perimetro è il doppio della diagonale del rettangolo.
  14. L’area di un rombo è 960 dm^2 e il rapporto tra le sue diagonali è 15/8. Determinare il perimetro e l’altezza del rombo.
  15. Un rombo ha una diagonale di 48 cm e il perimetro di 100 cm. Determinare la sua area, dopo aver osservato che il rombo è equivalente alla metà del rettangolo formato dalle sue diagonali. Determinare inoltre la distanza dai lati del punto di intersezione delle diagonali
  16. Determinare l’area e il perimetro di un trapezio rettangolo la cui altezza è i 14/5 della base minore ed è 4/5 del lato obliquo che è lungo 70 m.
  17. In un trapezio isoscele l’altezza è 4/15 della differenza delle basi, la base minore è 4/7 della maggiore e il perimetro è di 288 cm. Trovare l’area del trapezio e la lunghezza delle sue diagonali.
  18. Il perimetro del rettangolo ABCD è 11a; la base AB è i 17/5 dell’altezza BC, Determinare lati e area del rettangolo. Sulla base AB si prenda poi il segmento PB congruente a BC: si determini il segmento PD e, successivamente, si determini a in modo che sia 60 cm il perimetro del triangolo ADP.
  19. Nel parallelogrammo ABCD i lati AB e BC sono rispettivamente 60 cm e 45 cm; l’altezza DH è i 4/35 della somma di AB con BC. Calcolare la misura, in centimetri, dell’altezza relativa al lato AD.
  20. In un trapezio isoscele un lato è di 39 dm e la base di 72 dm; determinare l’area del triangolo e la lunghezza dell’altezza relativa a uno dei due lati congruenti.
  21. Determinare il perimetro di un triangolo isoscele sapendo che la somma della base e di un lato è 138 cm e che il lato è i 13/12 dell’altezza relativa alla base. (Indicare con x la misura dell’altezza).
  22. In un trapezio rettangolo le basi sono di 63 cm e di 42 cm; l’altezza è di 28 cm. determinare il perimetro e l’area del trapezio.
  23. La differenza delle basi di un trapezio isoscele è 60 cm e la somma è 68 cm. Determinare l’area del trapezio sapendo che il lato obliquo è di 34 cm.
  24. In un trapezio isoscele le basi sono lunghe rispettivamente 100 cm e 28 cm; l’altezza è di 48 cm. Determinare il perimetro e l’area del trapezio. Verificare che la diagonale è perpendicolare al lato obliquo.
  25. Il quadrilatero ABCD ha le diagonali, che si incontrano nel punto O, perpendicolari tra loro; si conosce che il perimetro del quadrilatero è di 56 cm, che 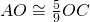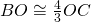AO \cong \frac 59 OC, BO \cong \frac 43 OC e BO \cong OD. Determinare l’area del quadrilatero ABCD.
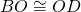  26. Determinare l’area del quadrilatero ABCD, avente le diagonali perpendicolari tra loro, sapendo che 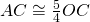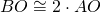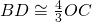AC \cong \frac 54 OC, BO \cong 2 \cdot AO, BD \cong \frac 43 OC, essendo O il punto di intersezione delle due diagonali AC e BD e sapendo che è

        \[\frac 53 AO+ 4OD- \frac 72 OB=2AC-6 \mbox { cm }\]

    . 1

 

 

 

Altri esercizi simili

(Questa pagina è stata visualizzata da 1417 persone)

Un pensiero riguardo “Problemi teorema di Pitagora”

  1. Pingback: Problemi sul teorema di pitagora | Matebook

Lascia un commento